3249. Test for Job
Mr.Dog was fired by his company. In
order to support his family, he must find a new job as soon as possible.
Nowadays, It's hard to have a job, since there are swelling numbers of the
unemployed. So some companies often use hard tests for their recruitment.
The test is like this: starting from
a source-city, you may pass through some directed roads to reach another city.
Each time you reach a city, you can earn some profit or pay some fee, Let this
process continue until you reach a target-city. The boss will compute the
expense you spent for your trip and the profit you have just obtained. Finally,
he will decide whether you can be hired.
In order to get the job, Mr.Dog
managed to obtain the knowledge of the net profit vi of all cities he may reach (a
negative vi indicates that money is spent rather
than gained) and the connection between cities. A city with no roads leading to
it is a source-city and a city with no roads leading to other cities is a
target-city. The mission of Mr.Dog is to start from a source-city and choose a
route leading to a target-city through which he can get the maximum profit.
Input. The input
file includes several test cases.
The first
line of each test case contains 2 integers n
and m (1 ≤
n ≤ 100000, 0 ≤ m ≤ 1000000) indicating the number
of cities and roads.
The next n lines each contain a single integer.
The i-th line describes the net profit of the city i, vi (0 ≤ |vi| ≤
20000)
The next m lines each contain two integers x, y
indicating that there is a road leads from city x to city y. It is
guaranteed that each road appears exactly once, and there is no way to return
to a previous city.
Output. The
output file contains one line for each test cases, in which contains an integer
indicating the maximum profit Dog is able to obtain (or the minimum expenditure
to spend)
|
Sample input |
Sample output |
|
6 5 1 2 2 3 3 4 1 2 1 3 2 4 3 4 5 6 |
7 |
РЕШЕНИЕ
графы – наибольший путь в
ациклическом графе
Анализ алгоритма
В задаче
необходимо найти наибольший путь в ациклическом графе. Значения выгоды vi могут
быть также отрицательными. Стартовым может быть только город, в который не
ведут дороги. Финальным – тот, из которого дороги не исходят.
Обозначим
через cost[i] выгоду i-го города, через dp[i]
максимальную выгоду, которую получит путешественник, начав свой путь из i (пусть i и не обязательно стартовый город). Если из вершины v не исходят дороги, то dp[v] = cost[v].
Пусть
сыновьями вершины v будут v1, …, vk. Тогда
dp[v] = cost[v] + max(dp[v1], …, dp[vk])
Введем
новую вершину 0 и соединим ее со всеми стартовыми вершинами. Положим cost[0] = 0.
Запускаем поиск в глубину из вершины 0, для каждой вершины i
пересчитываем dp[i]. Ответом задачи будет значение dp[0].
Пример
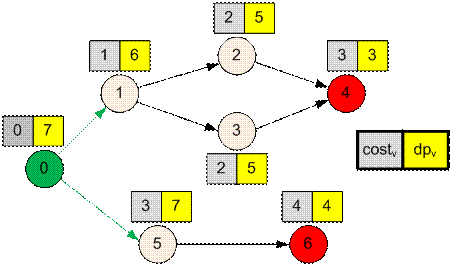
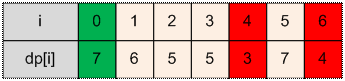
Реализация алгоритма
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cstring>
#define INF
0x8080808080808080LL
#define MAX
100010
using namespace std;
vector<int> g[MAX];
long long cost[MAX];
long long dp[MAX];
int
in[MAX];
int n, m,
i, u, v;
long long dfs(int v)
{
if (dp[v] !=
INF) return dp[v];
long long best = INF;
dp[v] = cost[v];
for(int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
dfs(to);
best = max(best,dp[to]);
}
if (best !=
INF) dp[v] += best;
return dp[v];
}
int main(void)
{
while(scanf("%d %d",&n,&m) == 2)
{
memset(cost,0,sizeof(cost));
memset(in,0,sizeof(in));
for(i = 1;
i <= n; i++)
scanf("%lld",&cost[i]);
for(i = 0;
i < MAX; i++)
g[i].clear();
for(i = 1;
i <= m; i++)
{
scanf("%d
%d",&u,&v);
g[u].push_back(v);
in[v]++;
}
memset(dp,0x80,sizeof(dp));
for(i = 1;
i <= n; i++)
if (in[i]
== 0) g[0].push_back(i);
dfs(0);
printf("%lld\n",dp[0]);
}
return 0;
}